Topologia e... Bottiglie - Matematica e Scienze - Curiosità Matematiche

 Topologia e... Bottiglie

Cos'è la topologia?

La topologia è una branca della matematica che si occupa dello studio delle proprietà degli oggetti matematici che non cambiano quando viene effettuata una deformazione senza "strappi", "sovrapposizioni" o "incollature". Due oggetti per i quali è possibile trasformare l'uno nell'altro e viceversa tramite tale tipo di deformazione sono detti omeomorfi. Un esempio molto famoso di omeomorfismo è tra due oggetti quotidiani, che non penseremmo mai possano avere una relazione matematica che li lega, ovvero una tazza ed una ciambella:

La "ciambella", il cui nome più adatto sarebbe "toro", è in realtà fondamentale: in topologia gli oggetti hanno un diverso "genere" in base al loro omeomorfismo con una sfera, o un toro, o un 2-toro (toro a 2 buchi), o un 3-toro e così via. In pratica, ci si rende facilmente conto che il genere è in base ai buchi dell'oggetto. Ma attenzione: non sono il tipo di buchi che definiamo comunemente come tali! Prendiamo sempre l'esempio della tazza: diremmo che ha due buchi, uno per il manico e l'altro per contenitore, eppure è omeomorfa ad un toro. Questo perché i buchi topologici sono quelli che, per spiegarlo in maniera semplice, possono essere attraversati da una parte all'altra. 

Superfici non-orientabili: Nastro di Möbius e Bottiglia di Klein

In topologia una superficie non è orientabile se ha una faccia sola e se e solo se contiene un Nastro di Möbius. Tale oggetto, scoperto da August Ferdinand Möbius (1790-1868), è ottenibile incollando due estremità di un rettangolo dopo aver girato di 180 gradi una di esse. Il Nastro di Möbius, oltre ad avere una sola faccia, ha quindi un solo lato. Sottostante una rappresentazione di M.C. Escher. Si noti come le formiche stiano camminando sulla stessa faccia.

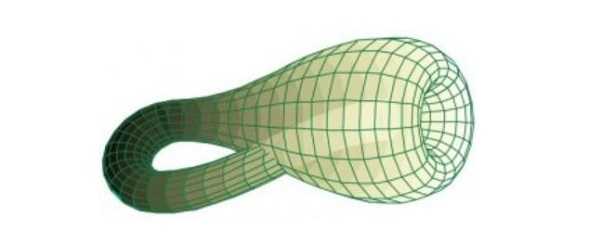
Un'altra interessante superficie non-orientabile è la Bottiglia di Klein, scoperta da Felix Christian Klein (1849-1925). E' ottenuta accostando due nastri di Möbius per il loro unico lato. Si può notare come accostando qualsiasi oggetto per uno dei loro lati quest'ultimo si perde. Perciò la bottiglia di Klein è una superficie non orientabile senza lati e con una sola faccia. 

A vederla sorge però la lecita domanda: il punto di intersezione tra la bottiglia e il collo ricurvo della stessa non è un lato? La risposta è che in realtà si tratta di un oggetto che per esistere con le giuste proprietà richiederebbe quattro dimensioni spaziali. In quel caso il collo non intersecherebbe la bottiglia; una formica 4D che vi cammina sopra attraverserebbe la faccia senza problemi. Purtroppo vivendo in un Universo tridimensionale la rappresentazione nella figura sovrastante è il meglio che possiamo fare. 

Rimaniamo sull'esempio della formica: si noti come essa può arrivare in ogni punto della bottiglia senza mai attraversare un bordo, quindi un lato (tenendo sempre conto della quadridimensionalità). L'interno e l'esterno della Bottiglia di Klein sono un'illusione dovuta alle nostre abitudini, similmente a come la tazza ha in realtà un buco solo; topologicamente se in un oggetto non esiste un lato da attraversare allora non è possibile definire né il suo interno né il suo esterno. 

Ancora una volta ringrazio il canale youtube Numberphile per l'ispirazione che mi ha dato a scrivere delle bellezze della matematica e lo consiglio nuovamente per chi volesse approfondire. In particolare la passione dimostrata dal matematico Clifford Stoll nelle sue spiegazioni è inimitabile.

https://www.youtube.com/watch?v=AAsICMPwGPY&ab_channel=Numberphile

https://www.youtube.com/c/numberphile

Fonti: wikipedia.org; youtube.com/c/numberphile

Scritto e redatto da Gennaro Fregola